NOMBRES (THÉORIE DES) - Nombres p-adiques

NOMBRES (THÉORIE DES) - Nombres p-adiques

On peut aborder l’étude d’un problème diophantien (cf. équations DIOPHANTIENNES) en commençant par chercher les solutions modulo p , un nombre premier quelconque: on est alors devant un problème plus facile, car Z/p Z est un corps ^{[cf. DIVISIBILITÉ]}. Cette méthode ne donne qu’une information insuffisante pour le problème initial; on la raffine en étudiant les équations modulo p ^m pour tous les entiers m 閭 1. L’anneau Z/p ^m Z n’est pas un corps, mais ses propriétés arithmétiques sont beaucoup plus simples que celles de Z: c’est un anneau fini qui a un seul idéal premier (engendré par la classe de p ); les autres idéaux sont les puissances de l’idéal premier.

Supposons maintenant qu’on connaisse une solution x ^m 捻 Z/p ^m Z du problème modulo p ^m ; pour tout k 諒 m , on en déduit une solution x ^k mod p ^k au moyen de l’application canonique évidente:

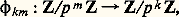provenant de l’application identique de Z. Ces considérations nous conduisent à introduire les suites (x ^m ) telles que x ^m 捻 Z/p Z pour tout m et x ^k = 﨏^km (x ^m ) pour k 諒 m . L’ensemble Z^p de ces suites est ainsi une partie du produit:

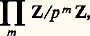et c’est même un sous-anneau pour la structure d’anneau produit (car les 﨏^km sont des homomorphismes d’anneaux); on dit que c’est la limite projective des anneaux Z/p ^m Z. L’anneau Z^p ainsi défini s’appelle l’anneau des entiers p-adiques ; la méthode d’approche d’un problème diophantien envisagée plus haut consiste à étudier d’abord le problème dans Z^p . Dans cet article, on donne les principales propriétés arithmétiques de cet anneau.

1. Généralités

Le noyau de l’homomorphisme canonique ZZ^p est formé des entiers divisibles par toutes les puissances de p ; il est donc réduit à0, et l’homomorphisme considéré est injectif et permet d’identifier Z à un sous-anneau de Z^p . La surjection canonique ZZ/p ⁿ Z se décompose en l’injection de Z dans Z^p suivie de la projection de Z^p dans le facteur Z/p ⁿ Z; on voit ainsi que cette dernière projection est surjective; son noyau est l’ensemble des entiers p- adiques (x ^m ) tels que x ⁿ = 0, ce qui donne x ^m = 0 pour m 諒 n et x ^m 捻 p ⁿ Z/p ^m Z pour m 礪 n ; autrement dit, ce noyau est l’ensemble des entiers p- adiques multiples de p ⁿ . On obtient ainsi l’isomorphisme:

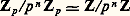pour tout entier n 閭 1.

Pour n = 1, cela montre que Z^p /p Z^p est un corps, donc que l’idéal p Z^p engendré par p est maximal. Si un entier p- adique x = (x ^m ) n’appartient pas à p Z^p , chacune de ses composantes x ^m est inversible dans le facteur correspondant Z/p ^m Z et (x ^{m -1}) est inverse de x dans Z^p ; ainsi l’idéal maximal p Z^p est exactement l’ensemble des éléments non inversibles de Z^p , et c’est donc le seul idéal maximal: l’anneau Z^p est local ^{[cf. ANNEAUX ET ALGÈBRES]} et son corps résiduel est Z^p /p Z^p 力 F^p , corps à p éléments. Les puissances successives de l’idéal maximal forment une suite décroissante (p ^m Z^p ) d’idéaux dont l’intersection est visiblement0; le plus grand de ces idéaux est p ⁰Z^p = Z^p . La multiplication par p ⁿ est injective dans Z^p ; il suffit de le vérifier pour n = 1, et px = 0 équivaut à px ^m = 0 dans Z/p ^m Z pour tout m , ce qui donne:

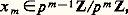d’où x ^m-1 = 0. L’anneau Z^p s’applique donc bijectivement sur l’idéal p ⁿ Z^p , et l’ensemble U = Z^p 漣 p Z^p de ses éléments inversibles s’applique bijectivement sur:

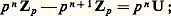on voit ainsi que l’ensemble Z ^p 漣0 est réunion disjointe des p ⁿ U (n 捻 N). Autrement dit, tout entier p- adique non nul x s’écrit d’une seule manière sous la forme p ⁿ u avec n 捻 N et u 捻 U entier p- adique inversible; l’entier naturel n s’appelle la valuation p-adique de x et se note v^p (x ). Si x = p ^m u et y = p ⁿ v sont des entiers p- adiques non nuls, avec u 捻 U et v 捻 U, on a: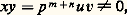

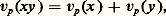car u v est encore inversible, donc Z^p est un anneau intègre ; on voit en même temps que:

et on peut vérifier par ailleurs l’inégalité:

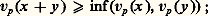ces deux propriétés de la valuation p- adique restent vraies même si x ou y est nul lorsque l’on pose v^p (0) = + 秊, élément abstrait ajouté à N avec les propriétés habituelles: on a n 麗 + 秊 et n + (+ 秊) = + 秊 pour tout n 捻 N.

Considérons un idéal non nul face=F9828 a de Z^p ; si n est la borne inférieure des valuations des éléments de face=F9828 a, on voit sans peine que face=F9828 a est l’idéal engendré par p ⁿ . Ainsi les seuls idéaux de Z^p sont (0) et les p ⁿ Z^p ; en particulier Z^p est un anneau principal et il n’a qu’un seul idéal premier non nul p Z^p : un tel anneau s’appelle un anneau de valuation discrète ^{[cf. ANNEAUX COMMUTATIFS]}. La décomposition en facteurs premiers d’un entier p- adique x est de la forme x = p ⁿ u avec n = ^vp (x ) et u 捻 U.

Il y a une autre structure intéressante sur l’anneau Z^p . On peut en effet considérer chaque Z/p ^m Z comme un anneau topologique discret et munir:

de la topologie produit; on obtient ainsi un anneau topologique compact, comme produit d’ensembles compacts (cf. théorème de Tychonoff, in TOPOLOGIE GÉNÉRALE). Comme les applications canoniques 﨏^km sont continues, Z^p est une partie fermée de cet anneau produit; c’est donc encore un anneau topologique compact pour la topologie induite. Un système fondamental de voisinages de 0 pour la topologie produit est formé par les ensembles: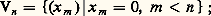

la trace de Vⁿ sur Z^p n’est autre que l’idéal p ⁿ Z^p qui est encore égal à l’ensemble des entiers p- adiques de valuation 閭 n . Pour tout entier p- adique x , on pose:

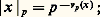ce dernier nombre s’appelle valeur absolue p-adique de x , et l’on a:

avec |x |^p = 0 si et seulement si x = 0. On voit alors que:

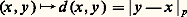est une distance (ultramétrique) sur Z^p (cf. espaces MÉTRIQUES); les remarques précédentes montrent que cette distance définit la topologie de Z^p . Notons maintenant que les isomorphismes:

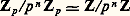montrent que Z est partout dense dans Z^p . Comme Z^p est complet (puisque compact), il est isomorphe au complété de Z pour la distance p -adique |y 漣 x |^p .

Soit S un système de représentants de F^p dans Z^p , c’est-à-dire un ensemble d’entiers p -adiques possédant exactement un élément dans chaque classe mod p Z^p . Par exemple, on peut prendre:

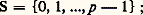mais nous verrons plus loin un autre système de représentants plus intéressant. Pour tout entier p- adique x , il existe un élément s ⁰ de S et un seul congru à x mod p Z^p ; on a x 漣 s ⁰ = px ¹ avec x ¹ 捻 Z^p . De même, il existe un couple unique d’éléments s ¹ 捻 S et x ² 捻 Z^p tels que x ¹ = s ¹ + px ², ce qui donne x = s ⁰ + ps ¹ + p ²x ²; en raisonnant par récurrence, on trouve pour tout n une manière unique d’écrire x sous la forme:

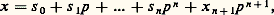avec s ⁱ 捻 S et x ⁿ⁺¹ 捻 Z^p . Lorsque n tend vers l’infini, le reste x ⁿ⁺¹ p ⁿ⁺¹ tend vers 0 dans Z^p ; on trouve donc un développement en série infinie:

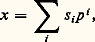avec des coefficients s ⁱ 捻 S; inversement, toute série de cette forme converge dans Z^p et définit un entier p -adique, comme on le voit, en appliquant le critère de Cauchy; notons d’ailleurs que, d’après l’inégalité ultramétrique:

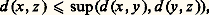une série converge dans Z^p dès que son terme général tend vers 0.

Au début du siècle, K. Hensel a introduit les nombres p- adiques en les définissant par des développements en série du type précédent.

Le corps des fractions Q^p de Z^p s’appelle le corps des nombres p-adiques ; il contient le corps Q des nombres rationnels comme sous-corps (autrement dit, c’est un corps de caractéristique 0). Chaque nombre p- adique peut s’écrire comme une fraction x /p ⁿ avec au numérateur un entier p- adique x et au dénominateur une puissance de p ; la valuation p- adique se prolonge à Q^p en posant:

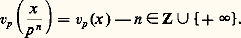On a encore:

pour x , y 捻 Q^p . On fait de Q^p un corps topologique localement compact en le munissant de la topologie pour laquelle Z^p est un sous-groupe additif ouvert (cf. TOPOLOGIE GÉNÉRALE - Algèbre topologique); cette topologie peut aussi être définie par la distance ultramétrique (x , y ) 料 d (x , y ) = |y 漣 x |^p correspondant à la valeur absolue |x |^p = p ^-v p ^(x) . Remarquons que Z^p n’est autre que la boule unité: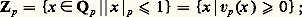

de même, l’idéal maximal p Z^p est défini par l’inégalité |x |^p 麗 1 ou aussi bien v ^p (x ) 礪 0. Le corps Q^p est complet , car il est localement compact, et Q est un sous-corps partout dense; donc Q^p est isomorphe au complété de Q pour la distance p- adique.

2. Équations p-adiques ; lemme de Hensel

Revenons aux considérations du début et étudions un système d’équations:

où 見 = 1, 2, ..., r et où les f size=1^見 sont des polynômes à coefficients dans Z^p ; on cherche les solutions (x ¹, x ², ..., x ^m ) dans (Z^p )^m . Par réduction modulo p ⁿ , on en déduit un système d’équations f size=1^見,n = 0 dans Z/p ⁿ Z. Pour que le système étudié ait une solution dans (Z^p )^m , il faut et il suffit que pour tout n le système réduit mod p ⁿ ait une solution dans (Z/p ⁿ Z)^m . En effet, une solution dans (Z^p )^m n’est autre qu’une suite de solutions mod p ⁿ pour tous les n , qui se correspondent par les applications canoniques 﨏^kn ; si Xⁿ 說 (Z/p ⁿ Z)^m désigne l’ensemble des solutions mod p ⁿ , on voit que l’image dans Xⁿ de l’image X des solutions dans (Z^p )^m est:

qui est non vide si chaque X^q est non vide (intersection décroissante d’ensembles finis non vides; en termes plus savants, on observe que X est limite projective des Xⁿ et que la limite projective d’une suite d’ensembles finis non vides est non vide).

De la même manière, on prouve que l’existence d’une solution primitive dans (Z^p )^m équivaut à l’existence d’une solution primitive mod p ⁿ pour tout n ; un élément primitif de (Z^p )^m , ou de (Z/p ⁿ Z)^m , est, par définition, un élément dont l’une des m coordonnées est inversible. Remarquons que l’existence d’une solution primitive dans (Z^p )^m équivaut encore à l’existence d’une solution différente de 0 dans (Q^p )^m ; on le voit en réduisant au même dénominateur.

Le résultat suivant donne une condition suffisante pour qu’un zéro mod p ⁿ d’un polynôme f 捻 Z^p [X¹, X², ..., X^m ] se relève en un zéro dans Z^p . Soit x 捻 (Z^p )^m tel que f (x ) 令 0 (mod p ⁿ ); s’il existe un indice j tel que:

il existe un élément y 捻 (Z^p )^m tel que f (y ) = 0 et y 令 x (mod p ^n-k ), où:

On construit y comme limite d’une suite (x ^q ) d’éléments de (Z^p )^m vérifiant:

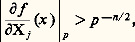
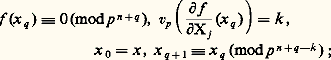l’existence d’une telle suite résulte du lemme suivant.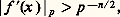

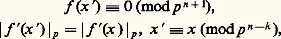Lemme. Soit f 捻 Z^p [X] et x 捻 Z^p tels que f (x ) 令 0 (mod p ⁿ ). Si:

il existe x 捻 Z^p tel que:

où k = v^p (f (x )).

Pour démontrer ce lemme, on cherche x sous la forme x = x + p ^n-k z et on utilise la formule de Taylor:

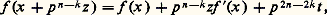où t est un entier p- adique; disons que f (x ) est multiple de p ⁿ et que la valuation de f (x ) est k , soit f (x ) = p ⁿ y et f (x ) = p ^k u avec y 捻 Z^p et u 捻 U, donc:

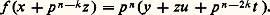Comme par hypothèse n 漣 2k 閭 1, il suffit de choisir z tel que y + zu soit multiple de p , c’est-à-dire z 令 漣 yu ^-1 (modp ); alors f (x + p ^n-k z ) est divisible par p ⁿ⁺¹ et:

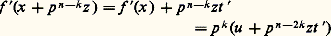a pour valuation k .

Appliquons ce résultat dans le cas où n = 1; on a alors nécessairement k = 0 et on voit que, si 﨡 捻 (F^p )^m est un zéro du polynôme:

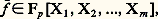déduit de f par réduction modulo p , et si une au moins des dérivées partielles premières de 肋 ne s’annule pas en 﨡 (zéro «simple»), alors il existe un zéro de f dans (Z^p )^m qui relève 﨡. Par exemple, si f est homogène de degré 2 (forme quadratique) et si son discriminant est inversible dans Z^p , 肋 est une forme quadratique non dégénérée à coefficients dans F^p ; lorsque p 2 tout 﨡 捻 (F^p )^m 漣0 tel que 肋 ( 﨡) = est une racine simple et se relève donc en un x 捻 (Z^p )^m tel que f (x ) = a . Lorsque p = 2, on montre de même que, si x est un élément primitif de (Z²)^m tel que f (x ) 令 a (mod 8), il existe y 捻 (Z²)^m tel que f (y ) = a et y 令 x (mod 4). Pour m = 1, ces résultats permettent de déterminer les éléments inversibles de Z^p qui sont les carrés; lorsque p 2, ce sont les éléments de U dont la classe mod p est un carré dans F^p ; nous étudierons plus loin les carrés de Z^p par une autre méthode.

Le lemme de Hensel est un résultat voisin du précédent et s’énonce ainsi: soit f 捻 Z^p [X] un polynôme à une indéterminée à coefficients entiers p- adiques; supposons donnée un décomposition 肋 = 﨏祥 de la réduction de f modulo p en produit d’un polynôme unitaire 﨏 de degré d et d’un polynôme 祥 étranger à 﨏; il existe un couple unique (g , h ) de polynômes g , h appartenant à Z^p [X] tels que f = gh , 凜 = 﨏, 凌 = 祥 et que g soit unitaire de degré d .

3. Structure du groupe multiplicatif Q^p

On sait que tout élément non nul de Q^p s’écrit d’une seule manière sous la forme p ⁿ u avec n 捻 Z et u 捻 U, groupe des éléments inversibles de Z^p ; cela donne immédiatement un isomorphisme Q^p 力 Z 憐 U. Il reste à étudier la structure du groupe U; on définit une filtration décroissante (Uⁿ ) de U en posant pour tout n 礪 0:

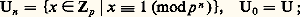ainsi Uⁿ est le noyau de l’homomorphisme canonique de U dans le groupe des éléments inversibles de Z/p ⁿ Z. Il est clair que U/U¹ 力 F^p , groupe cyclique d’ordre p 漣 1; pour n 閭 1, une bijection x 料 1 + p ⁿ x de Z^p sur Uⁿ applique p Z^p sur U^{n +1} et définit un isomorphisme de groupes:

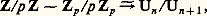en vertu de l’identité:

ainsi Uⁿ /Uⁿ⁺¹ est cyclique d’ordre p pour n 閭 1.

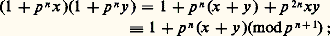De ces considérations on peut déduire qu’il existe un sous-groupe unique V de U isomorphe à F^p et que U est isomorphe au produit V 憐 U¹; le sous-groupe V est l’ensemble des entiers p -adiques x tels que x ^p-1 = 1, et V 聆0 est un système de représentants de F^p dans Z^p qui est stable par multiplication, c’est un système de représentants multiplicatifs (cf. chap. 1). Pour obtenir ces résultats, on considère U et U¹ comme limites projectives des suites de groupes (U/Uⁿ ) et (U¹/Uⁿ ) respectivement, et on est ramené à prouver l’existence d’un unique sous-groupe Vⁿ de U/Uⁿ isomorphe à F^p et tel que:

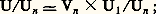comme U¹/Uⁿ est d’ordre p ^n-1 et que:

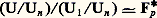est d’ordre p 漣 1 premier à p ^n-1 , on peut démontrer que U/Uⁿ est produit de U¹/Uⁿ par le sous-groupe des racines (p 漣 1)-ièmes de 1 en utilisant l’identité de Bezout ^{[cf. ANNEAUX COMMUTATIFS]}. Chemin faisant, nous avons démontré que le corps des nombres p -adiques Q^p contient les racines (p 漣 1)-ièmes de 1.

Il faut enfin élucider la structure du groupe U¹. Nous allons voir que U¹ est isomorphe au groupe additif Z^p si p est différent de 2, et à梁 1 憐 Z² si p = 2. Pour p 2, on choisit un élément a de U¹ qui n’appartient pas à U² et on considère l’homomorphisme x 料 a ^x de Z dans U¹; on a a = 1 + pu avec u 捻 U, donc a ^x = 1 + xpu + p ²t (t entier p -adique) par le développement du binôme, et, pour x premier à p , cela montre que a ^x est encore un élément de U¹ qui n’est pas dans U²; au contraire, pour x = p ^h , on trouve que a ^x est un élément de U^h+1 qui n’est pas dans U^h+2 , en remarquant que pour tout n la puissance p -ième d’un élément de Uⁿ 漣 Uⁿ⁺¹ appartient à Uⁿ⁺¹ 漣 Uⁿ⁺² . Ces résultats permettent de voir que l’image réciproque de Uⁿ⁺¹ dans Z est exactement p ⁿ Z; par conséquent, x 料 a ^x définit un homomorphisme injectif de Z/p ⁿ Z dans U¹/Uⁿ⁺¹ , et cet homomorphisme est même un isomorphisme, car les deux groupes ont le même nombre d’éléments. En passant à la limite projective pour n秊, on obtient l’isomorphisme cherché Z^p 轢黎 U¹; on notera encore a ^x l’image d’un entier p -adique x par cet isomorphisme. Dans le cas où p = 2, on observe d’abord que:

et on définit un isomorphisme de Z² sur U² à partir de l’homomorphisme x 料 a ^x de Z dans U² construit à l’aide d’un élément a de U² qui n’appartient pas à U³ (ainsi a est congru à 5 mod 8). En résumé, on a trouvé que le groupe multiplicatif Q^p est isomorphe à: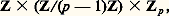

si p 2 et à :

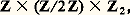si p = 2.

Nous sommes maintenant en mesure de déterminer quels sont les carrés dans Q^p . Pour p 2, on a:

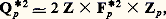car, 2 étant inversible dans Z^p , on a 2Z^p = Z^p ; on retrouve le fait qu’un élément inversible de Z^p est un carré si et seulement si son image dans F^p est un carré. Le groupe quotient Q^p /Q^{p 2} est isomorphe à:

c’est un groupe à 4 éléments qui admet pour système de représentants dans Q^p l’ensemble1, p , u , up où u est un entier qui n’est pas résidu quadratique modp .

Lorsque p = 2, on a: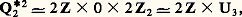

et alors:

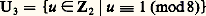est l’ensemble des carrés inversibles de Z²;

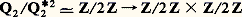est un groupe d’ordre 8 qui admet pour système de représentants1, 2, 3, 5, 6, 7, 10, 14 dans Q². Notons que Q^{p 2} contient U¹ si p 2 et U³ si p = 2; donc, c’est un sous-groupe ouvert de Q^p ; le groupe quotient Q^p /Q^{p 2} peut être considéré comme un espace vectoriel sur le corps à 2 éléments F², de dimension 2 ou 3 suivant que p 2 ou p = 2. Sur cet espace vectoriel, il y a une forme bilinéaire canonique, qui est symétrique et non dégénérée; elle est définie par le symbole de Hilbert (a , b ), a , b 捻 Q^p , qui vaut 1 ou 漣 1 suivant qu’il existe ou non un élément non nul de (Q^p )³ qui annule la forme quadratique Z² 漣 a X² 漣 b Y² (cf. DIVISIBILITÉ, théorie des NOMBRES - Nombres algébriques, formes QUADRATIQUES). À l’aide du symbole de Hilbert, on définit un invariant 﨎(f ) associé à toute forme quadratique f à coefficients dans Q^p ; si:

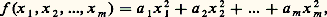dans une base orthogonale, on a:

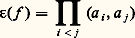et on peut montrer que 﨎(f ) ne dépend pas de la base orthogonale choisie. Pour que deux formes quadratiques à coefficients dans Q^p soient isomorphes, il faut et il suffit qu’elles aient même rang, même invariant 﨎 et que leurs discriminants aient la même classe dans Q^p /Q^{p 2}; on trouve ainsi 4 (resp. 8) classes de formes de rang 1 et 7 (resp. 15) classes de formes de rang 2 et enfin 8 (resp. 16) classes de formes de rang n 閭 3 si p 2 (resp. p = 2).

4. Analyse p-adique

On peut développer une théorie des fonctions analytiques de variables p -adiques en définissant de telles fonctions par des développements en séries entières convergentes (cf. FONCTIONS ANALYTIQUES - Fonctions analytiques d’une variable complexe).

Par exemple, la série exponentielle :

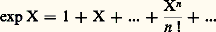converge dans le «disque ouvert» de Q^p défini par l’inégalité:

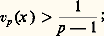en effet:

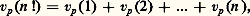et le nombre d’entiers k 諒 n tels que v^p (k ) 閭 r est égal à la partie entière [n/p ^r ] du nombre rationnel n/p ^r , ce qui donne:

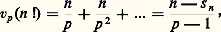en désignant par s ⁿ la somme des coefficients du développement p -adique de n (si n = a ⁱ p ⁱ avec 0 諒 a ⁱ 諒 p 漣 1, on a s ⁿ = a ⁱ ); on en déduit facilement que v^p (1/n !)/n converge vers 漣 1/(p 漣 1) pour n infini, c’est-à-dire que |1/n !|^1/n converge vers p ^1/(p size=1^漣1). On peut donc définir une fonction exponentielle x 料 exp x pour |x | 麗 p size=1^漣1/(p size=1^漣1); il est clair que l’on a:

et que la fonction exponentielle ne s’annule pas dans son disque de convergence: elle définit un homomorphisme de ce disque, qui est un sous-groupe du groupe additif de Q^p (à savoir p Z^p si p 2 et 4Z² si p = 2), dans le groupe multiplicatif de Q^p . C’est en fait un isomorphisme sur un sous-groupe de Q^p , comme on peut le montrer à l’aide de la fonction logarithme définie par la série: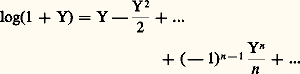

qui converge pour v^p (y ) 礪 0 et définit donc un logarithme dans U¹; on peut vérifier que:

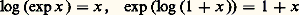pour v^p (x ) 礪 1/(p 漣 1) et, par suite, exp définit un isomorphisme de p Z^p sur U¹ si p 2 et de 4 Z² sur U² si p = 2: on retrouve les isomorphismes du chapitre 3.

Comme le corps Q^p est totalement discontinu, on ne peut espérer une théorie globale raisonnable pour les fonctions analytiques au sens habituel, c’est-à-dire définies localement par des développements en série. Il y a cependant une théorie globale pour les fonctions «strictement holomorphes»; donnons, par exemple, la définition des fonctions strictement holomorphes dans la «couronne»:

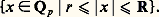Ce sont les fonctions définies par des développements de Laurent:

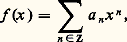qui vérifient la condition de convergence suivante: pour tout 福 捻 [r , R], |a ⁿ | 福ⁿ tend vers 0 lorsque n tend vers 梁 秊; l’espace L(r , R) de ces développements de Laurent est un espace de Banach sur le corps Q^p pour la norme (ultramétrique):

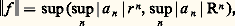et on peut y définir une multiplication qui en fait une algèbre de Banach. On démontre que L(r , R) est un anneau principal et que ses éléments irréductibles sont les polynômes unitaires irréductibles dont les racines (dans une clôture algébrique de Q^p ) ont des valeurs absolues dans l’intervalle [r , R], ainsi que les produits de ces polynômes par des éléments inversibles; ces derniers sont les développements de la forme:

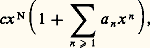avec |a ⁿ |r ⁿ 麗 1 et |a ⁿ |Rⁿ 麗 1 pour tout n . M. Lazard a généralisé ces résultats au cas d’une couronne «ouverte» (définie par des inégalités strictes) et a obtenu des théorèmes analogues à ceux de Weierstrass (développement en produit infini d’une fonction strictement méromorphe) et de Mittag-Leffler.

En s’inspirant de la théorie de Jacobi, J. Tate a élaboré une théorie analytique des fonctions elliptiques sur un corps p -adique. Soit q 捻 Q^p tel que 0 麗 |q | 麗 1, on considère le corps des fonctions strictement méromorphes dans Q^p 漣0 (couronne de rayons 0 et 秊) qui sont invariantes par la multiplication par q , c’est-à-dire f (qx ) = f (x ); on peut montrer que c’est un corps de fonctions algébriques d’une variable et que son genre est 1, c’est-à-dire qu’il s’identifie au corps des fonctions rationnelles sur une courbe elliptique. Cette théorie donne l’uniformisation de certaines courbes elliptiques sur Q^p ; plus récemment, M. Raynaud et D. Mumford ont étudié d’une manière analogue les variétés abéliennes et les courbes algébriques de genre 閭 2.

J. Tate a également donné une définition des espaces analytiques p -adiques qui permet d’étudier les fonctions analytiques de plusieurs variables. Les principaux théorèmes de la théorie des faisceaux cohérents (cf. FONCTIONS ANALYTIQUES - Fonctions analytiques de plusieurs variables) ont été établis pour ces espaces (J. Tate et R. Kiehl). Le renouveau d’intérêt pour l’analyse p -adique vient surtout de la démonstration par Dwork de la rationalité de la fonction zêta d’une variété algébrique sur un corps fini (cf. fonction ZÊTA); la méthode utilisée consiste à démontrer la rationalité d’une série formelle à coefficients entiers en étudiant ses propriétés comme fonction analytique p -adique (pour différents nombres premiers p ); les propriétés en question s’obtiennent, dans le cas de la fonction zêta, en appliquant la théorie de Fredholm p -adique (J.-P. Serre; cf. théorie SPECTRALE).

Il existe aussi une théorie des groupes de Lie p -adiques tout à fait analogue à celle des groupes de Lie réels ou complexes (cf. GROUPES - Groupes de Lie). Le résultat du chapitre 3 sur la structure de Q^p se généralise ainsi: tout groupe de Lie commutatif de dimension n sur Q^p contient un sous-groupe ouvert isomorphe à (Z^p )ⁿ ; si le groupe considéré est compact, c’est une extension d’un groupe fini par (Z^p )ⁿ . La théorie des représentations linéaires pour les groupes de Lie p -adiques a été développée par F. Bruhat; dans le cas commutatif, on dispose de la transformation de Fourier comme dans le cas classique et le groupe dual du groupe additif Q^p est isomorphe à Q^p . Signalons enfin l’existence d’une théorie des fonctions sphériques p -adiques et les travaux de F. Bruhat et J. Tits sur la structure des groupes algébriques p -adiques.

5. Extensions

On connaît beaucoup d’autres anneaux de valuation discrète que les anneaux Z^p ; nous pouvons citer l’anneau k [[T]] des séries formelles à une indéterminée à coefficients dans un corps k , ou l’anneau local d’un point régulier sur une courbe algébrique (ou sur une courbe analytique complexe; cf. GÉOMÉTRIE ALGÉBRIQUE). Si A est un anneau de valuation discrète de corps des fractions K et si 神A est l’unique idéal premier non nul de A, les idéaux de A sont 0 et les 神ⁿ A (n 捻 N); tout élément x 0 de K s’écrit d’une seule manière sous la forme x = 神ⁿ u où n 捻 Z et où u est un élément inversible de A; la valuation de x est l’entier v(x ) = n et l’application v : KZ est un homomorphisme surjectif de groupes vérifiant l’inégalité v(x + y ) 閭 inf (v(x ), v(y )). Inversement, la donnée d’une valuation discrète v : KZ détermine un sous-anneau:

où l’on a posé v(0) = + 秊, qui est un anneau de valuation discrète et dont l’idéal maximal est l’ensemble des éléments de valuation 礪 0. La valuation définit une valeur absolue ultramétrique: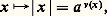

où a est un nombre réel fixé appartenant à l’intervalle ]0, 1]; on a:

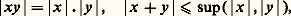et |x | ne s’annule que pour x = 0. Dans le cas où K est complet pour la topologie définie par cette valeur absolue, il possède des propriétés très semblables à celles de Q^p ; pour qu’il soit localement compact, il faut et il suffit qu’il soit complet et que le corps résiduel k = A/ 神A soit fini (cf. théorie des NOMBRES - Nombres algébriques). Si A est un anneau de valuation discrète complet et si L est une extension finie de son corps des fractions K, on démontre que la fermeture intégrale B de A dans L est encore un anneau de valuation discrète complet et que c’est un A-module libre de rang [L:K]; désignons par 神 un générateur de l’idéal maximal de A (une «uniformisante») et par w la valuation définie par B; l’entier e = w ( 神) s’appelle l’indice de ramification de L sur K. La valeur absolue de K se prolonge d’une manière unique à L. Considérons un anneau de valuation discrète complet A; supposons que son corps des fractions K soit de caractéristique 0 et son corps résiduel k de caractéristique p 礪 0. Alors, l’injection canonique de Z dans A (resp. de Q dans K) se prolonge par continuité en:

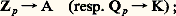l’entier e = v(p ), où v est la valuation définie par A, s’appelle l’indice de ramification absolue de A. On démontre (I. S. Cohen) que, pour tout corps parfait k de caractéristique p , il existe un anneau de valuation discrète complet A absolument non ramifié (c’est-à-dire d’indice de ramification absolue égal à 1, ce qui signifie que l’idéal maximal de A est p A) dont le corps résiduel est k ; cet anneau est unique à isomorphisme (unique) près, et sa construction se fait au moyen des vecteurs de Witt ; ainsi Z^p est l’anneau de valuation discrète complet absolument non ramifié de corps résiduel F^p .

Si A est un anneau de valuation discrète complet de caractéristique un nombre premier p , alors son corps résiduel k est aussi de caractéristique p , et on démontre qu’il admet dans A un système de représentants qui est un sous-corps (les représentants multiplicatifs sont également additifs; cf. chap. 3); on en déduit, en utilisant des développements de type hensélien par rapport aux puissances d’une uniformisante, que A est isomorphe à l’anneau des séries formelles k [[T]]. Il en est de même si k est de caractéristique 0.

L’analyse p -adique se généralise en remplaçant Q^p par un corps valué complet ultramétrique quelconque. Les résultats et les méthodes sont les mêmes (sauf ceux qui font intervenir les propriétés arithmétiques particulières à Q^p ).

Encyclopédie Universelle. 2012.